Hash에 대해서
1. Hash 란
임의의 데이터를 고정된 크기의 정수로 변환해주는 것. Hash 또는 Hashing이라 한다.
Hash 함수는 이런 역할을 하는 Hash algorithm을 구현한 함수를 말한다.
2. Hash의 용도
- 데이터를 저장함에 있어 빠르게 검색을 할 수 있도록 indexing 하는 key로 사용.
(만약 어떠한 데이터를 저장하는데 저장된 이후 빠르게 검색하게 하기 위해서는 데이터의 index를 만들고 해당 index에 데이터를 저장하면 된다. 이후 검색할때는 이 index에서 바로 값을 찾아낼 수 있다. hash값은 바로 이러한 index를 만들때 사용한다. ) - 데이터의 무결성을 확인하는데 사용된다. 예를 들어 다운로드한 파일의 무결성을 확인할때 업로더가 정상적인 hash값을 적어두면, 다운로더는 동일한 hash 함수를 통해 hash값을 얻어낸 후 값이 동일한지 확인하여 무결성을 확인한다.
- 데이터 무결성 확인할때 사용하는 주 용도가 전자서명이다.
3. Hash 함수(알고리즘)
Hash 함수의 특징으로 항상 한 쪽 방향으로만 연산된다.
즉, 해시된 값을 분석함으로써 원본값을 찾아내거나 해시 함수를 추출해내는 reverse engineering은 필요가 없다.
이상적인 해시함수는 이러한 분석에 의해 추론할 수 없어야 한다.
또한, 우수한 해시 함수는 서로 다른 두 개의 입력에 대해 동일한 해시 값을 만들지 않는 것이다. (이는 불가능함)
서로 다른 값에 대해서 동일한 해시 값이 리턴되는것을 해시 충돌이라 한다.
이러한 충돌 위험성이 적은 해시 함수가 훌륭한 해시 함수로 평가된다.
유명한 Hash 알고리즘으로 MD(MD1, MD2, MD5 등), SHA(SHA-1, SHA-2) 알고리즘이 있다.
참고로 MD5 해쉬는 1996년부터 취약점이 발견되었고, SHA-1 해쉬도 공격이 이미 감지되었다. 따라서 정말 중요한것은 SHA-2 해쉬를 사용하는 것을 권장한다고 한다.
4. Key-Value Table의 2가지 방법
4.1. Direct Addressing Table
key-value로 데이터를 배열에 저장하는데 key값을 직접 배열 index로 사용하고 해당 배열에 value를 저장하는 방식이다.
구조가 매우 단순하고, O(1)의 시간에 검색이 가능한 장점이 있다.
하지만 key값의 범위가 큰데 비해 저장되는 데이터가 적다면 불필요하게 메모리 소모가 크다.
예를 들어 key값의 범위가 최대 500이라면 우선 500만큼의 배열을 만들어야 한다.
4.2. Hash Table
Hash table은 Direct Addressing Table의 단점(불필요한 메모리공간)을 hash 함수로 극복한 방법이다.
Hash table의 경우 value를 hash함수를 통해 key값을 만들어내고 이 key값을 배열의 index로 사용한다.
Direct Addressing Table의 경우 input으로 들어오는 key값의 범위에 따라서 메모리 사용량이 결정되는데 Hash table의 경우 hash 함수의 구현에 따라 저장할 배열의 크기가 달라진다.
Hash table은 서로 다른 value에 대해서 유일한 index를 보장하지 못한다.
이렇게 다른 값에 대해 동일한 hash 함수값이 리턴되는걸 해시 충돌이라 하고 이러한 해시 충돌이 발생했을때 해결하는 여러가지 방법이 있다.
5. Java의 HashTable 과 HashMap
5.1. 정의
HashMap과 HashTable을 정의한다면 아래와 같다고 한다.
Key에 대한 Hash값을 사용하여 값을 저장/조회 하고, Key-Value 쌍의 개수에 따라 동적으로 크기가 증가하는 associate array.
이 associate array를 지칭하는 다른 용어로 Map, Dictionary, Symbol Table 등이 있는데, HashMap에서는 내부적으로 Map이라는 용어를 사용하고, HashTable은 내부적으로 Dictionary 라는 용어를 사용한다고 한다.
5.2. JDK에서의 차이
HashTable은 JDK 1.0부터 있던 Api이고, HashMap은 JDK 2.0에 추가된 Collection Framework에 추가된 Api이다.
HashTable, HashMap 모두 Map 인터페이스를 구현하고 있으므로 둘이 제공하는 기능은 동일하다.
HashTable은 하위 호환성 유지때문에 존재하고 있고, 사실상 업데이트로 되지 않는 반면 HashMap의 경우 성능 개선이 지속적으로 이뤄지고 있다.
따라서 둘의 성능을 비교하는 것은 의미가 없다.
HashTable과 HashMap의 주요 차이점은 아래와 같다.
- HashTable은 모든 메서드가 동기화되어 있으므로 성능상 단점이 있다.
- HashMap은 보조 해시 함수를 사용하고 있어 HashTable에 비해서 해시 충돌이 덜 발생해 성능이 좋다.
6. Hash 분포와 Hash 충돌
서로다른 객체 X, Y에대해서 X.equals(Y)가 false일때 X.hashCode() != Y.hashCode() 를 무조건 만족한다면 이 Hash함수는 완전한 해시 함수(perfect hash functions)라고 할 수 있다.
만약 구분되는 객체의 종류가 유한한 경우(ex - boolean, integer, long) 객체의 값 자체를 key로 삼을 수 있고, 완전 해시 함수의 대상으로 삼을 수 있다.
하지만 String이나 일반적인 객체를 대상으로 완전 해시 함수를 만드는것은 사실상 불가능하다.
적고 빠른 연산으로 동작하는 완전 해시 함수가 존재한다 하더라도 HashMap에서 사용할 수 있는것은 아니다. (사실 hashCode() 메서드는 int값을 리턴하게 하고 있으므로 완전 해시 함수 자체가 존재할 수 없음. 세상의 모든 객체를 2^32개로 표현할 수 없으므로)
그 이유는 Direct Addressing Table의 단점과 동일한데 값을 저장하기 위한 배열의 크기가 2^32개나 존재해야 하기 때문이다.
위와 같은 메모리 이슈로 HashMap을 비롯하여 Hash함수를 사용하는 associate array 구현체들은 내부적으로 M개 크기의 배열만 사용한다.
int index = X.hashCode() % M;
관련 코드는 위와 같은데 나머지 연산을 통해 index의 범위를 0~(M-1)로 한정한다.
이 경우 서로 다른 해시 코드를 가지는 객체에 대해서도 1/M 확률로 같은 해시 버킷을 사용하는 문제가 있다.
서로 다른 객체가 동일한 Hash값을 리턴하는것을 Hash충돌이라 하는데, 위 경우는 메모리 절약때문에 서로 다른 Hash값에 대해서 동일한 index값을 리턴하는 또 다른 문제가 발생한다. 이 문제는 또다른 형태의 Hash 충돌이다.
이렇게 또 다른 형태의 Hash충돌이 발생하더라도 Key-Value값을 잘 저장하고 조회할 수 있도록 하는 방법이 여러가지가 있는데 대표적으로 Open Addressing, Separate Chaining 이 있다.
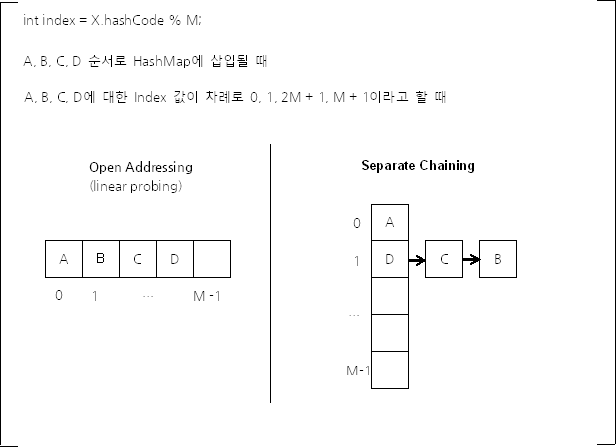
6.1. Separate Chaining
각 배열의 index는 같은 해시 버킷을 연결한 LinkedList의 Head이다.
즉, 서로 다른 객체가 같은 hash값을 가지게 되는 경우 해당 index에서 LinkedList 형태로 연결된다.
LinkedList 방식이라 처음 위치를 찾는 과정 이후에는 모든 탐색/삽입/삭제가 LinkedList의 구현을 따르게 된다.
참고로 Java 8에서 HashMap에서는 LinkedList가 아니라 Red-Black Tree로 바뀌었다고 한다.
6.2. Open Addressing
데이터를 삽입하려고 하는데 이미 해시 버킷이 사용중이라면 다른 해시 버킷에 데이터를 삽입한다.
즉, hash 값을 index 위치로 하는것을 기본으로 하지만 해당 index에 있는 값이 반드시 맞다고 할 수는 없다.
데이터를 저장/조회할 해시 버킷을 찾을때 Linear Probing, Quadratic Probing 등의 방법을 사용한다.
6.2.1. Linear Probing
충돌이 발생했을때 바로 다음 index에 데이터를 저장하는 방식이다.
다음 index로 이동한 이후에 또 충돌이 발생하면 또 다시 다음 index에 값을 저장하는 과정을 반복한다.
// k는 index, i는 충돌시 1씩 증가하는 값, m은 배열 크기
h(k,i) = (k+i) mod m

Linear Probing은 간단하지만 primary clustering 이라는 문제점이 있다.
이는 비슷한 위치에서 충돌이 자주 발생할때 하나의 데이터 덩어리를 이루게 되어 특정 위치에 데이터가 밀집하는 현상을 말한다. 이 현상이 발생하면 탐색 시간이 크게 늘어난다.
6.2.2. Quadratic Probing
primary clustering 현상을 방지하기 위해 index 증가를 1차식으로 하지 않고 2차식 형태로 만든것이다.
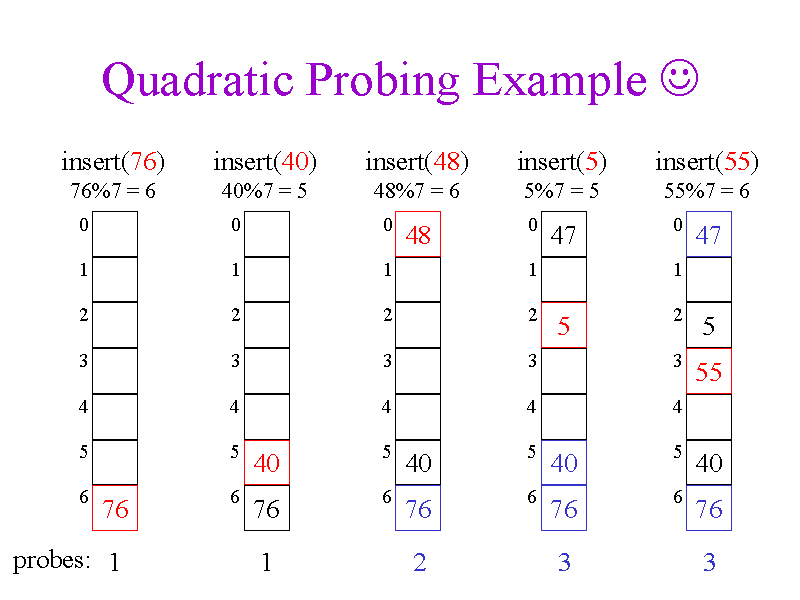
위는 간단한 예로 해쉬 함수는 h(k,i) = (k+i^2) mode m 형태를 취한 것이다.
Quadratic Probing은 primary clustering이 발생하지 않지만 secondary clustering 이라는 또 다른 문제가 발생한다.
이는 처음 시작 hash 값이 같을때 그 이후의 해쉬값이 모두 동일한 값으로 계산되어 충돌이 반복적으로 일어나는것을 말한다.
6.3. HashMap의 구현
JDK의 HashMap은 Separate Channing 을 사용한다.
Open Addressing은 데이터 삭제할때 효율적이기 어려운데 HashMap은 삭제가 빈번할 수 있기 때문이다.
또한, HashMap에 저장된 데이터 개수가 일정 개수 이상으로 많아지면 Open Addressing이 Separate Channing보다 느리다고 한다.
[참고 문서]
댓글남기기